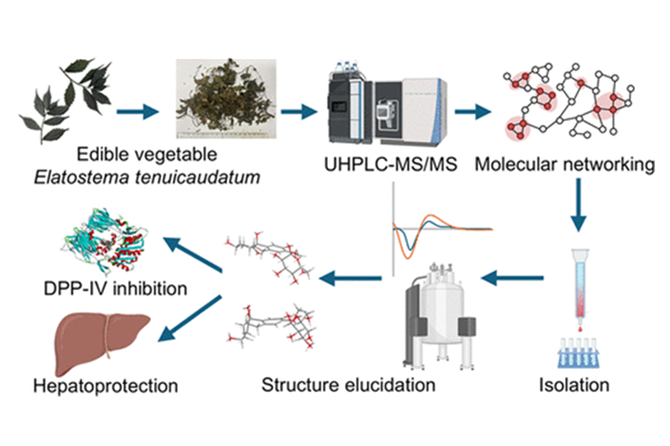
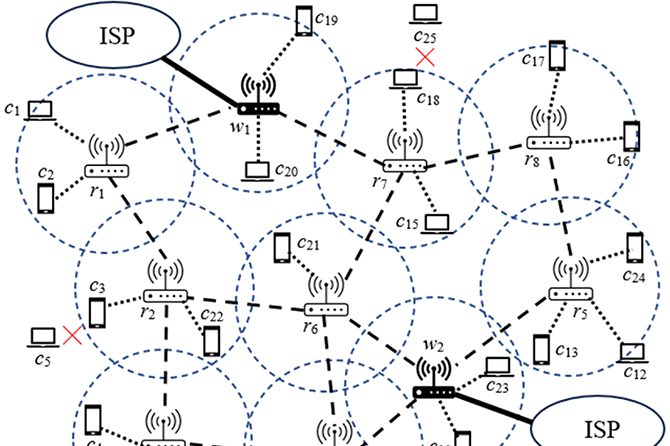
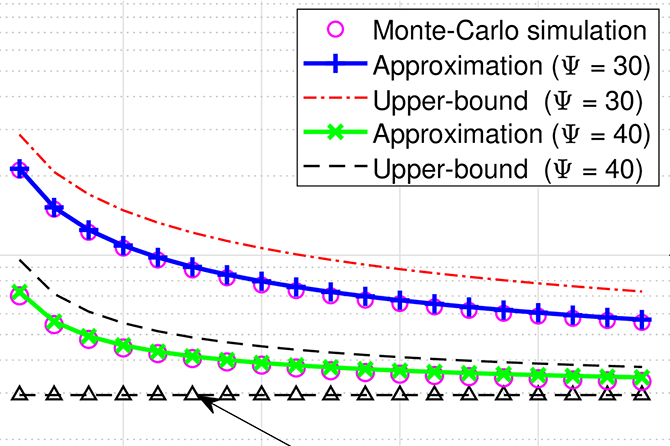
Quoc-Dung Tran Huynh, Su-Jung Hsu, Truc-Ly Thi Duong, Hui-Kang Liu, Ta-Wei Liu, Man-Hsiu Chu, Yun-Han Wang, Dang-Khoa Nguyen, Thuy-Tien Thi Phan, Nguyen-Khanh Huynh Tran, Thanh-Hoa Vo, Hsiao-Yang Hsi, Tz-Wei Yeh and Ching-Kuo Lee
Publication year
2018
Publisher
Journal of Mathematical Analysis and Applications
In this paper, we study the hyperstability for the general linear equation in the setting of quasi-Banach spaces. We first extend the fixed point result of Brzdek et al. [5, Theorem 1] in metric spaces to b-metric spaces, in particular to quasi-Banach spaces. Then we use this result to generalize the main results on the hyperstability for the general linear equation in Banach spaces to quasi-Banach spaces. We also show that we can not omit the assumption of completeness in [5, Theorem 1]. As a consequence, we conclude that we need more explanations to replace a normed space by its completion in the proofs of some results in the literature.